When people talk about datastructures and algorithms they often hype them up so high that they seem like fanciful super-abstractions for Real Programmers.
The reality is much more down to earth.
Consider a data structure we’re already familiar with: the Vec. A Vec is a struct with a specific set of functions implemented on it.
Functions like .push, .pop, the ability to access an item at a specific index, and so on.
For Snake, we can use a Vec to hold the body positions of the snake. Imagine for a second that we have a small board, one that only had one row and many columns.
The Snake in this situation can only move right, so we only store the x-index for each snake segment: vec![0,1,2].
If the snake needs to move to the right we have two options:
Option 1
Option 1 is that we can modify the values, either by mutating or by replacing the whole snake with a new, moved snake.
The code for this in our small snake grid isn’t too bad. The snake always moves to the right, so we always add one to the value stored in the segment.
fn main() {
let mut snake = vec![0,1,2];
dbg!(&snake);
for segment in snake.iter_mut() {
*segment += 1;
}
dbg!(&snake);
}
If we run that code, the debug output gives us a moved snake.
[src/main.rs:3] &snake = [
0,
1,
2,
]
[src/main.rs:7] &snake = [
1,
2,
3,
]
This approach quickly becomes complicated though, and even in this small example we can see that as the snake gets longer, we actually keep the vast majority of values that already exist. A snake with segments 0..10 will become a snake with segments 1..11. The numbers [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] all exist in both snakes, yet we’re mutating all 10 values.
Option 2
Instead we can go with Option 2.
If we think about all of the values that haven’t changed then we need to remove the item at index 0, and push a new value onto the end of the Vec.
We can push the new value onto the end of the Vec, but pop only operates on the end as well, so if we try to push and pop with a Vec, then we end up with the same snake.
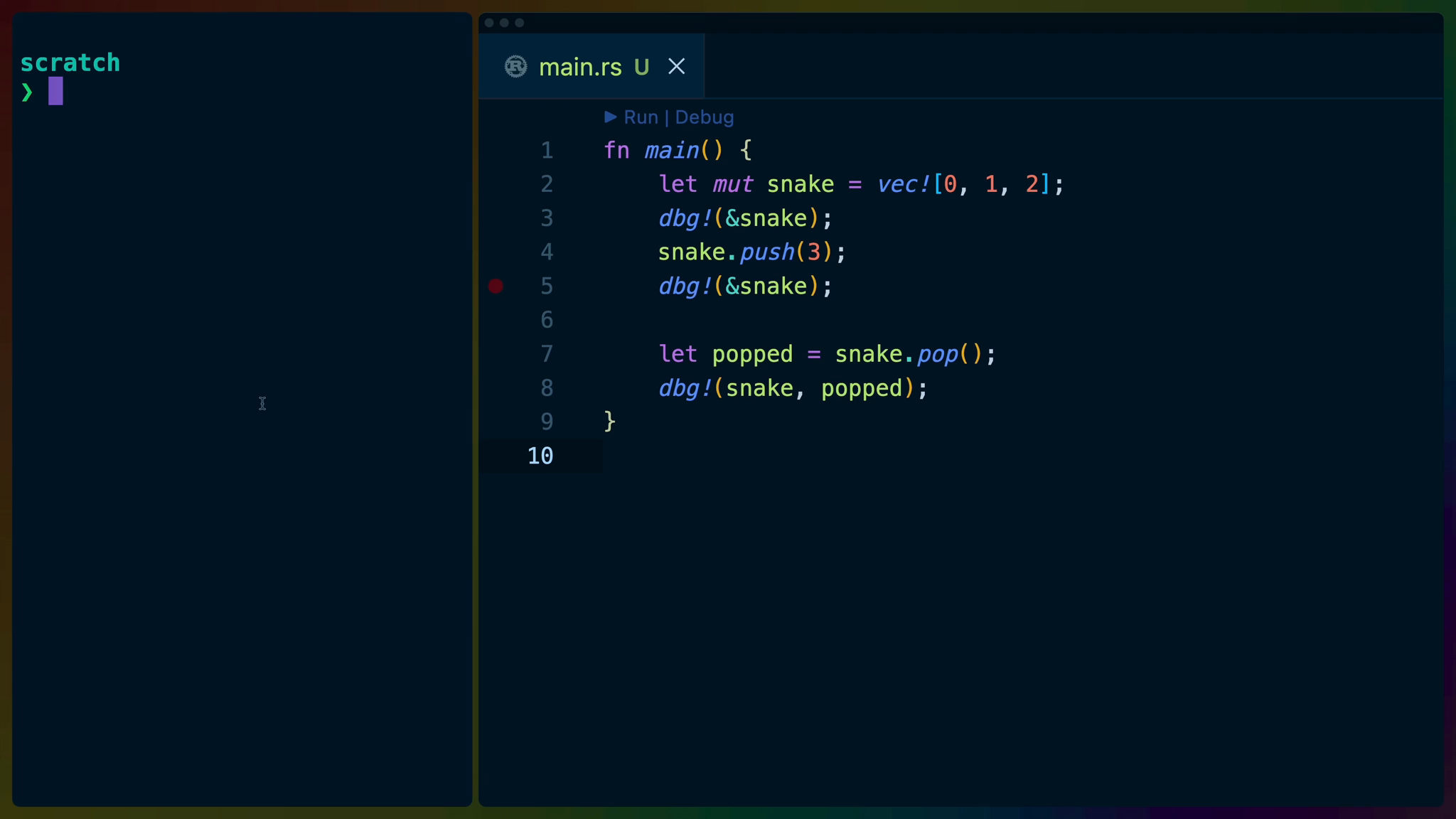
fn main() {
let mut snake = vec![0,1,2];
dbg!(&snake);
snake.push(3);
dbg!(&snake);
let popped = snake.pop();
dbg!(snake, popped);
}
The output if we run that code is
[src/main.rs:3] &snake = [
0,
1,
2,
]
[src/main.rs:5] &snake = [
0,
1,
2,
3,
]
[src/main.rs:8] snake = [
0,
1,
2,
]
[src/main.rs:8] popped = Some(
3,
)
Instead we can use a datastructure called a VecDeque.
At a high level, we can think of a VecDeque as a Vec with some additional functions.
It’s a lot like coffee. An Espresso is Espresso in a cup, and an Espresso Macchiato is Espresso with milk foam on top in a cup.
The functions we care about are push_back and pop_front.
If we modify our earlier code, we can see this in action.
use std::collections::VecDeque;
fn main() {
let mut snake = VecDeque::from([0,1,2]);
dbg!(&snake);
snake.push_back(3);
dbg!(&snake);
let popped = snake.pop_front();
dbg!(snake, popped);
}
and running the code confirms our snake positions.
[src/main.rs:5] &snake = [
0,
1,
2,
]
[src/main.rs:7] &snake = [
0,
1,
2,
3,
]
[src/main.rs:10] snake = [
1,
2,
3,
]
[src/main.rs:10] popped = Some(
0,
)
In this way we can push new positions onto the “back” (also known as the last value) of the snake, and pop them from the “front” (or 0 index).
The VecDeque has additional benefits as well. It allows us to think less about how the values for more complicated 2d positions in a grid need to be modified. For example: Our snake is going to move in four directions and turn, making everything more complicated.
We only need to focus on the next board position the snake is going to.
and when the snake eats food we only need to forget to call pop_front and the snake will grow one size!
An ergonomic change
I also personally find it confusing to use “front” for the tail of the snake, and “back” for the head of the snake, so we’ll store our snake segments in “head-to-tail order”: [2,1,0] instead of “tail-to-head” order: [0,1,2]. This matches the .back function on VecDeque to the tail of the snake, and the .front function to the head, and the 0 index to the head as well, since we need to access the head far more than we need to access the tail.