So now we have a left board shift done and working. To implement the other three directions we can think about them as left shifts as well. A downward shift is a left-shift applied to a board rotated 90 degrees. A right-shift is a left-shift applied to a board rotated 180 degrees, and a up-shift is a left shift applied to a board rotated 270 degrees.
With this knowledge, as long as we can order the tiles to appear as if we're applying a left-shift, we don't have to change the logic comparing values for merging.
We'll move the logic for a left-shift into an impl for BoardShift. We will have to have a BoardShift to tell which direction to handle in the first place, so putting the logic here makes sense although we could also write a set of independent functions that wasn't on the BoardShift struct.
We'll move the sort closure into a sort method. Changing the types to take shared references to self, and two Positions. We take shared references because we aren't mutating anything, so don't need exclusive access or to own the data. We're effectively telling the sort function "hey, take a look at these and tell me what you think, but they're not yours"
impl BoardShift {
fn sort(&self, a: &Position, b: &Position) -> Ordering {
match Ord::cmp(&a.y, &b.y) {
Ordering::Equal => Ord::cmp(&a.x, &b.x),
ordering => ordering,
}
}
fn set_column_position(
&self,
position: &mut Mut<Position>,
index: u8,
) {
position.x = index;
}
fn get_row_position(&self, position: &Position) -> u8 {
position.y
}
}
We're calling our other functions set_column_position and get_row_position because when we rotate the board with the sort, the row could be the x or the y. So instead of calling it set_x we call it set_column to match how we're thinking about the board. x and y are implementation details where our algorithm only makes us think about rows and columns no matter which direction we're shifting in.
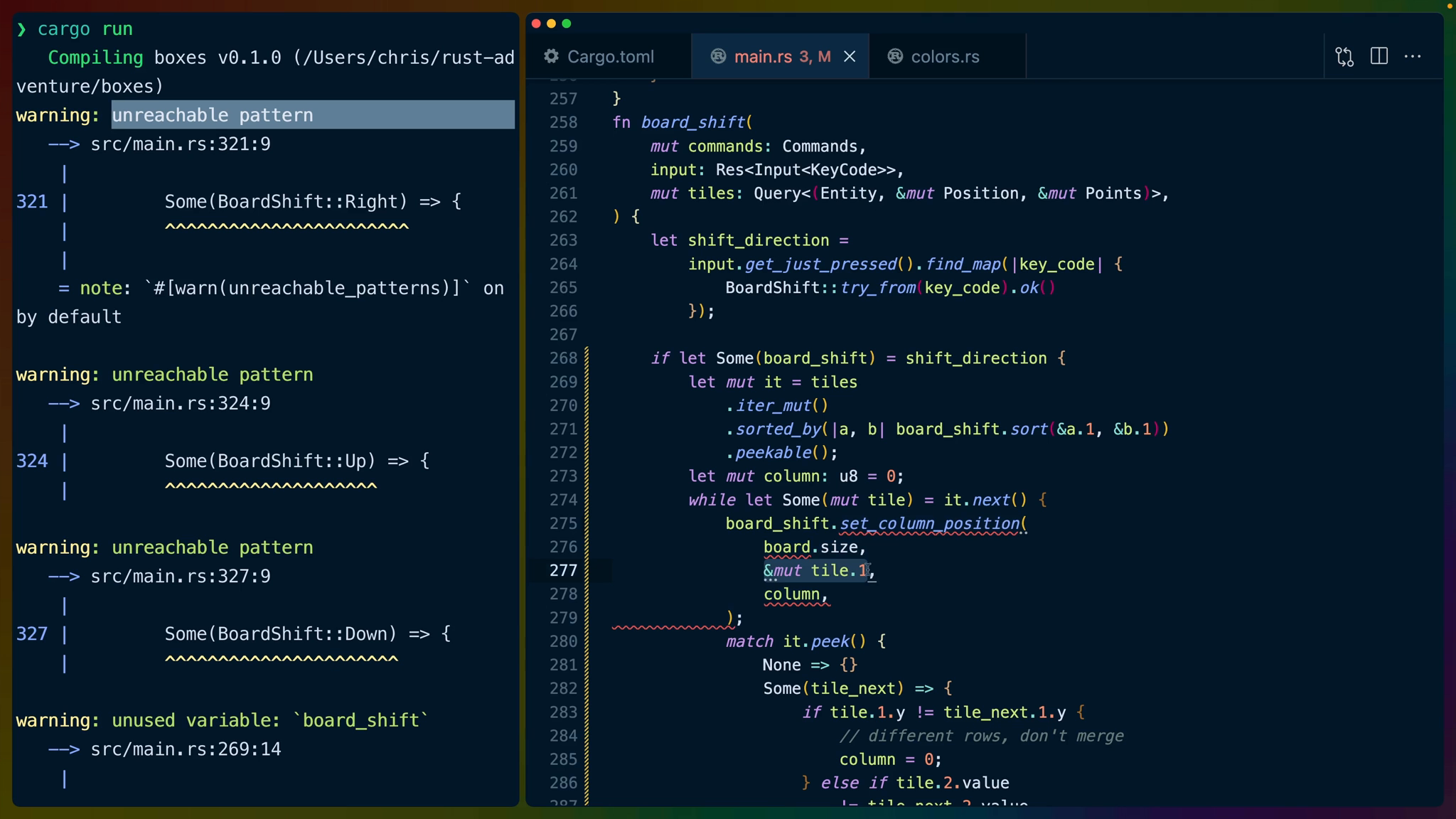
To apply the changes we'll change our match shift_direction to be a bit more general and match on the Some structure, leaving the board shift in a variable for all variants of the enum.
Some(board_shift) =>
This causes the other exact Some matches to be "unreachable patterns" so we can remove them. They're unreachable because the structure of Some(variable) will match all valid BoardShift variants before they get a chance to match the exact matches further below.
This brings our match down to "if Some, do something, else do nothing". Rust has an idiomatic way of dealing with exactly this situation: if-let.
if-let does the same kind of matching as match with the difference that we only care about a single possible match. if shift_direction matches the structure Some() then let board_shift equal the inner value. In this case if we don't match, we do nothing, but we could use an else to do something for anything that doesn't match the if-let.
if let Some(board_shift) = shift_direction {...}
The sort also changes to accept a board_shift.sort. Our method implicitly accepts a reference to self, so calling the .sort method on a board shift value already allows us to access it. We do need to explicitly pass in the two &Position arguments though. They're shared references so when we pass them in we make that clear using &.
This will let us use a different sort for each direction while not polluting the surrounding logic.
let mut it = tiles
.iter_mut()
.sorted_by(|a, b| board_shift.sort(&a.1, &b.1))
.peekable();
Inside of our iteration, we replace setting the column with set_column_position. We pass in a mutable reference to the Position because it needs to be mutated, but we also need it back.
while let Some(mut tile) = it.next() {
board_shift.set_column_position(
board.size,
&mut tile.1,
column,
);
...
}
Now that we know about if-let we can use it for the it.peek as well since in the None case we do nothing.
if let Some(tile_next) = it.peek() {
The only change left to make in our board_shift function is to replace any row accesses with .get_row_position.
if let Some(tile_next) = it.peek() {
if board_shift.get_row_position(&tile.1)
!= board_shift
.get_row_position(&tile_next.1)
{
// different rows, don't merge
column = 0;
} else if tile.2.value != tile_next.2.value
{
// different values, don't merge
column = column + 1;
} else {
// merge
// despawn the next tile, and
// merge it with the current
// tile.
let real_next_tile = it.next()
.expect("A peeked tile should always exist when we .next here");
tile.2.value = tile.2.value
+ real_next_tile.2.value;
commands
.entity(real_next_tile.0)
.despawn_recursive();
// if the next, next tile
// (tile #3 of 3)
// isn't in the same row, reset
// x
// otherwise increment by one
if let Some(future) = it.peek() {
if board_shift
.get_row_position(&tile.1)
!= board_shift
.get_row_position(&future.1)
{
column = 0;
} else {
column = column + 1;
}
}
}
}
At this point we haven’t made any functional changes.
In sort, we can use Rust Analyzer here to fill out the arms of the match.
match self {
BoardShift::Left => todo!(),
BoardShift::Right => todo!(),
BoardShift::Up => todo!(),
BoardShift::Down => todo!(),
}
sort continues in the same way we started. We sort each set of tiles for each BoardShift direction so that it looks like we're operating on all of them in the same way we did in the left shift. This is just like we tilted our head 90 degrees and looked at the board as if it was a left shift again. In this way we can treat a downward board shift as a left shift, if we look at the board 90 rotated.
fn sort(&self, a: &Position, b: &Position) -> Ordering {
match self {
BoardShift::Left => {
match Ord::cmp(&a.y, &b.y) {
Ordering::Equal => Ord::cmp(&a.x, &b.x),
ordering => ordering,
}
}
BoardShift::Right => {
match Ord::cmp(&b.y, &a.y) {
std::cmp::Ordering::Equal => {
Ord::cmp(&b.x, &a.x)
}
a => a,
}
}
BoardShift::Up => match Ord::cmp(&b.x, &a.x) {
std::cmp::Ordering::Equal => {
Ord::cmp(&b.y, &a.y)
}
ordering => ordering,
},
BoardShift::Down => {
match Ord::cmp(&a.x, &b.x) {
std::cmp::Ordering::Equal => {
Ord::cmp(&a.y, &b.y)
}
ordering => ordering,
}
}
}
}
As we expand the set_column_position we realize that we need the board size to make sure we stop the tiles at the far ends of the board.
To do that we'll add a query_board to our board_shift system.
query_board: Query<&Board>,
And grab the existing board with .single
let board = query_board.single();
Then we get to see the pattern in setting column positions. When shifting left, we set the x to the current index, which starts at 0. When shifting right we set x to the current index, but starting at the end of the board instead of the beginning. When the board is rotated so that y is the column, it behaves the same.
fn set_column_position(
&self,
board_size: u8,
position: &mut Mut<Position>,
index: u8,
) {
match self {
BoardShift::Left => {
position.x = index;
}
BoardShift::Right => {
position.x = board_size - 1 - index
}
BoardShift::Up => {
position.y = board_size - 1 - index
}
BoardShift::Down => {
position.y = index;
}
}
}
get_row_position has the least amount of logic out of all three methods. It returns whichever value represents the row. In a left-shift or right-shift, that's y. In an up or down-shift, that's x.
We can list all four options out as we've been doing in the other examples.
fn get_row_position(&self, position: &Position) -> u8 {
match self {
BoardShift::Left => position.y,
BoardShift::Right => position.y,
BoardShift::Up => position.x,
BoardShift::Down => position.x,
}
}
or we can use Rust's ability to match on multiple patterns using |.
fn get_row_position(&self, position: &Position) -> u8 {
match self {
BoardShift::Left | BoardShift::Right => position.y,
BoardShift::Up | BoardShift::Down => position.x,
}
}
With the additional logic in place, we can now run the game and see all four directions working.